Т.В. Чернова
Межрегиональная дифференциация денежных доходов населения
Ростов н/Д: Изд-во СКНЦ ВШ, 2002. - 192 с.

Предыдущая

Оглавление

Следующая

3. Статистическая оценка региональной дифференциации денежных доходов населения

3.2. Метод главных компонент в анализе региональной дифференциации среднедушевых денежных доходов

Во многих статистических исследованиях [6, 28, 52, 68, 157] содержится описание метода главных компонент и особенности его применения в различных областях знания. В изложении приведенных источников, рассмотрим основные положения компонентного анализа.

Модель компонентного анализа имеет следующий вид:

z_j = a_j1 F₁+ a _j2 F₂  +….+a_jn F_{n ,}             (j=1,2,….n),

где a_jn  – факторная нагрузка (вес) главной компоненты j-го параметра; F_n  – значение главной компоненты для i-го объекта.

Каждый из наблюдаемых параметров линейно зависит от n некоррелированных между собой новых компонентов (факторов) F₁,F₂,...,F_n. При этом число факторов объявляется равным числу исходных параметров, а представленная модель, по сути, есть система преобразования одних параметров в другие. Первая главная компонента представляет собой линейную комбинацию исходных параметров, учитывающую максимум их суммарной дисперсии. Вторая главная компонента не коррелирует с первой и учитывает максимум оставшейся дисперсии и т.д. до тех пор, пока вся дисперсия не будет учтена.

Сумма дисперсий всех компонент равна сумме дисперсий всех исходных параметров. Материалом для анализа является корреляционная матрица исходных параметров, на диагонали которой стоят единицы.

Формальное описание метода главных компонент заключается в следующем. Первый фактор F₁ и нагрузки a_i1 находим из условия минимума функционала:

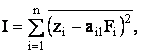
при условии, что F₁ задан в стандартной форме.

Факторные нагрузки a_ij, соответствующие минимуму функционала I, должны равняться коэффициентам корреляции    r(z_i,F₁) между соответствующими параметрами и первым фактором F₁. При этом F₁ должен соответствовать максимуму функционала I¢:

В компонентном анализе производится вращение исходной системы координат к новой системе в полном пространстве параметров – ортогональное преобразование, при котором каждый из n параметров выражается через n главных компонент. Целью вращения является максимизация дисперсий квадратов исходных факторных нагрузок по переменным для каждой компоненты. В результате вращения отдельные коэффициенты при компонентах могут изменяться так же, как вклады каждой из компонент, однако дисперсия каждого параметра и суммарный вклад главных компонент остаются неизменными. При вращении системы координат находится такое ее положение, которое для каждой строки (или столбца) матрицы увеличивает большие факторные нагрузки и уменьшает малые, т.е. увеличивает число близких к нулю элементов матрицы, чем способствует выявлению факторной структуры в более четкой, рельефной форме. Процедура вращения методом «кваримакс» обеспечивает выполнение этой операции для строк матрицы главных компонент, а методом «варимакс» – для столбцов этой матрицы [157, с.318, с.326].

Обычно на практике оставляют небольшое число компонент, особенно если каждая очередная компонента дает максимально возможный вклад в суммарную дисперсию параметров. В этом заключается важнейшее свойство данного метода.

Полученные результаты требуют интерпретации, суть которой состоит в отыскании причины, лежащей в основе взаимосвязанного изменения признаков. «Интерпретация распределения значений факторов по объектам зависит от интерпретируемости матрицы факторных нагрузок, которая определяет, какие исходные параметры дают основной вклад в тот или иной фактор»[52, с.6].

Выделение из двадцати трех факторных признаков основных, образующих в определенном сочетании главные компоненты, осуществлялось последовательно по всем группам параметров для всех регионов России в целом, а также для экономических районов. Именно главные компоненты оказывают непосредственное влияние на уровень формирования среднедушевых денежных доходов населения регионов.

При проведении исследования процедуры компонентного анализа выполнялись с помощью программной системы статистического анализа и обработки данных STATISTICA фирмы StatSoft Inc.

На основе исходных параметров была рассчитана матрица парных коэффициентов корреляции, которая служит количественным выражением степени связи между каждой парой из рассматриваемых 23 показателей (табл.1. Прил.1). Анализ корреляционной матрицы позволяет выделить наиболее тесно взаимосвязанные пары показателей; это показатели Х₃-Х₁₉; Х₃-Х₂₃; Х₅-Х₇; Х₅-Х₈; Х₅-Х₁₀, Х₇-Х₈; Х₇-Х₁₀; Х₇-Х₁₁; Х₇-Х₂₀; Х₈-Х₁₀; Х₁₁-Х₁₀; Х₁₁-Х₂₀; Х₁₁-Х₁₅; Х₁₁-Х₁₇; Х₁₁-Х₁₈; Х₁₅-Х₁₇; Х₁₅-Х₁₈; Х₁₇-Х₁₈; Х₁₇-Х₁₉; Х₁₈-Х₁₉; Х₁₈-Х₂₃; Х₁₉-Х₂₃.

С помощью факторного анализа выявляется структура взаимосвязей между группами показателей. Преобразование корреляционной матрицы в матрицу факторных нагрузок (табл.3.1) осуществляется методом главных компонент.

Таблица 3.1

Главные компоненты для региональных параметров

(по России)

В основе определения главных компонент лежит ряд  собственных значений исходной корреляционной матрицы. Колонки таблицы соответствуют главным компонентам, а строки – параметрам. Таким образом, элементы любой из строк – это коэффициенты при компонентах в линейном выражении для соответствующего параметра. Кроме того, они являются коэффициентами корреляции между параметрами и главными компонентами.

Вклад каждой компоненты в суммарную дисперсию сопоставляется с некоторым «порогом», на основе чего, после выделения четырех главных компонент, факторизация прекращается. Сумма квадратов элементов строки есть дисперсия данного параметра, а суммы квадратов элементов по столбцам показывает дисперсию главных компонент. Здесь видно, как реализуется основное свойство компонентного анализа – максимальный вклад каждой последующей компоненты в суммарную дисперсию. В частности, в приведенном примере первые четыре главные компоненты учитывают около 70 % дисперсии.

Вклад каждой из компонент в описание суммарной дисперсии всего набора региональных параметров определяется как сумма квадратов факторных нагрузок по столбцу, деленная на полную суммарную дисперсию параметров, которая в нашем случае равна 23.

В табл. 3.1 первая из выделенных компонент обусловливает 30,5% дисперсии восьми параметров (Х₅, Х₇, Х₈, Х₁₀, Х₁₁, Х₁₅, Х₁₈, Х₂₀), вторая компонента – двух параметров (Х₁₉, Х₂₃), третья компонента – одного параметра (Х₃), четвертая компонента – одного параметра (Х₁₄). Количество высоких нагрузок у первой и второй компоненты резко отличаются, что затрудняет их интерпретацию.

С целью улучшения интерпретации результатов желательно выравнять нагрузки двух первых компонент, для этого проведем вращение системы координат вокруг ее центра по критерию «варимакс» (критерий Кайзера) [157]. Результат преобразования представлен в табл. 3.2.

Таблица 3.2

Главные компоненты (после вращения)

Параметры	1 компонента	2 компонента	3 компонента	4  компонента	Сумма квадратов нагрузок
Х1	0,186	-0,168	-0,161	0,411	0,257
Х2	0,401	0,389	0,235	-0,576	0,700
Х3	-0,133	0,835	-0,247	0,325	0,882
Х4	-0,534	0,313	-0,386	0,349	0,654
Х5	0,939	0,054	0,035	0,146	0,908
Х6	0,441	-0,202	0,611	0,124	0,625
Х7	0,886	0,173	0,194	0,084	0,860
Х8	0,909	0,075	-0,040	-0,082	0,841
Х9	0,627	-0,155	-0,190	0,315	0,553
Х10	0,845	0,171	0,206	0,189	0,822
Х11	0,585	0,663	0,295	-0,126	0,885
Х12	-0,088	0,014	0,557	-0,109	0,329
Х13	0,334	0,030	0,038	0,700	0,605
Х14	0,148	-0,163	0,498	0,352	0,420
Х15	0,229	0,612	0,500	-0,376	0,819
Х16	0,050	0,316	0,628	-0,072	0,502
Х17	0,130	0,810	0,332	-0,209	0,827
Х18	0,191	0,924	0,107	-0,172	0,933
Х19	0,033	0,917	0,006	-0,174	0,873
Х20	0,794	0,098	0,135	0,013	0,658
Х21	0,605	-0,069	-0,096	-0,374	0,520
Х22	-0,181	-0,234	0,195	0,369	0,262
Х23	-0,155	0,869	-0,265	-0,118	0,865
Вклад	5,949	5,232	2,336	2,102	15,620
Процент суммарной дисперсии	25,86	22,74	10,16	9,14	67,90

В табл. 3.2 представлен результат преобразования матрицы главных компонент после ее вращения, где количество высоких нагрузок первой и второй компоненты выравнялось, что облегчает их интерпретацию. Матрицы главных компонент до вращения и после вращения в равной степени полно отражают информацию, представленную в корреляционной матрице, т.к. значения общностей, вычисляемых как суммы факторных нагрузок по соответствующей строке, совпадают.

Первая компонента обусловливает дисперсию параметров Х₅, Х₇, Х₈, Х₁₀, Х₂₀, т.е. число предприятий и организаций в регионе, стоимость основных фондов региона, инвестиции в основной капитал и страховые выплаты в регионе. Обобщая, можно сказать, что первая главная компонента отражает уровень концентрации капитала в регионе и определяет его производственный и финансовый потенциал.

Вторая главная компонента обусловливает, главным образом дисперсию Х₃, Х₁₇, Х₁₈, Х₁₉ и Х₂₃ показателей – это доля мужского населения в регионе, объем платных услуг на душу населения, среднемесячная заработная плата, среднемесячная пенсия и среднедушевой прожиточный минимум.

Совокупность выделенных параметров характеризует уровень показателей доходов, определяемых структурой населения региона и развитостью сферы платных услуг.

Третью компоненту можно определить как различия регионов в степени их специализации на отрасли, оказывающие услуги и отрасли, производящие товары, поскольку именно этот параметр (Х₆) вносит существенный вклад в дисперсию показателей.

Четвертая компонента выражает уровень развития сферы обращения, что в значительной мере обусловлено значениями индекса физического объема розничной торговли (Х₁₄) и индекса физического объема продукции сельского хозяйства региона (Х₁₃).

Факторную структуру главных компонент, полученную после вращения матрицы факторных нагрузок, хорошо видно на рис. 3.2.

Рис.3.2. Факторная структура главных компонент

В прил. 2 приводятся графики факторных нагрузок для экономических районов, построенные на основе выделенных главных компонент. Исследования, проведенные по выделению главных компонент из анализируемой совокупности региональных факторов для экономических районов, во многом дали схожие результаты.

Компонентный анализ региональных параметров производился для следующих 7 экономических районов: Центрального, Поволжского, Северо-Кавказского, Уральского, Западно-Сибирского, Восточно-Сибирского, Дальневосточного. Не удалось произвести расчеты по Северо-Западному, Северному, Волго-Вятскому и Центрально-Черноземному районам. Причина в недостаточной, по количеству объектов информации. Процедура выделения главных компонент для экономических районов осуществлялась в такой же последовательности, что и для РФ в целом. Результаты расчетов приведены в прил. 2.

Для Центрального экономического района общий вклад  в описание дисперсии региональных параметров первых четырех компонент равен 75,8 %.

Первая главная компонента определяется тесно взаимосвязанными показателями – число предприятий и организаций (Х₅), стоимость основных фондов (Х₇), число фермерских хозяйств (Х₉), инвестиции в основной капитал (Х₁₀), страховые выплаты (Х₂₀) и прирост по вкладам в регионе (Х₂₁), что интерпретируется как уровень концентрации производственного и финансового капитала в регионе. Вклад первой компоненты обусловливает 38,8% дисперсии выделенных параметров.

Вторая главная компонента описывает дисперсию параметров – валовой региональный продукт (Х₁₁), розничный товарооборот (Х₁₅) – и равна 15,7 %. Взаимосвязь этих показателей можно определить как уровень развития материального производства.

Третья компонента интерпретируется как уровень развития торговли и сферы услуг в регионе, она определяется взаимосвязью двух параметров – индекс физического объема розничной торговли региона (Х₁₄), объем платных услуг на душу населения (Х₁₇) – и обусловливает 10,9 % суммарной дисперсии.

Четвертая компонента характеризует уровень развития образования в регионе, поскольку наибольший вклад в собственное значение компоненты вносит именно число студентов высших и средних учебных заведений в регионе (Х₁). Четвертая компонента дает 10,3% суммарной дисперсии параметров.

В Поволжском экономическом районе общий вклад  в описание дисперсии региональных параметров четырех выделенных главных компонент равен 88,8%. Первая компонента обусловливает 46,56%, вторая – 16,37%, третья – 14,36%, четвертая – 11,48% суммарной дисперсии. На основании анализа выделенных параметров в каждой компоненте их можно интерпретировать следующим образом.

Первая главная компонента характеризует уровень развития сферы материального производства и услуг в регионе, что выражается в тесной взаимосвязи показателей валового регионального продукта на душу населения (Х₁₁), розничного товарооборота на душу населения региона (Х₁₅), объемами бытовых и платных услуг (Х₁₆, Х₁₇).

Вторая главная компонента интерпретируется как уровень концентрации производства и развития сельского хозяйства в регионе, что определяется значением показателей – число предприятий и организаций в регионе (Х₅) и индексом физического объема продукции сельского хозяйства (Х₁₃).

Третья компонента обусловлена социально-демографическими показателями (Х₂, Х₃) и интерпретируется как структура населения региона.

Четвертая компонента определяется как уровень динамики цен, поскольку обусловлена значением индекса потребительских цен в регионе (Х₂₂).

Для Северо-Кавказского экономического района вклад каждой из четырех выделенных компонент всего набора региональных параметров в суммарную дисперсию соответственно равен – 38,31%; 21,21%; 19,1% и 9,8%, что в сумме составляет 88,4%. Выделенные компоненты интерпретируем, исходя из сложившейся взаимосвязи показателей.

Первая главная компонента интерпретируется как концентрация производственного и финансового капитала в регионе, обусловившая эффективность его функционирования, что выражается во взаимосвязи всех показателей группы ресурсной обеспеченности региона и валового регионального продукта на душу населения в регионе (Х₁₁).

Вторая главная компонента характеризуется специализацией региона, что определяет, в свою очередь, высокий уровень безработицы (Х₄, Х₆).

Третья компонента интерпретируется как уровень показателей доходов населения региона, что определяется низкими размерами средней заработной платы (Х₁₈) и средней пенсии (Х₁₉).

Четвертая компонента выражает уровень развития сельского хозяйства в регионе, поскольку в значительной мере определяется индексом физического объема продукции сельского хозяйства (Х₁₃).

Для Уральского экономического района суммарный вклад главных компонент равен 21,5 из 23, что дает 93,5% в описание дисперсии параметров.  

Первая из выделенных компонент обусловливает 35,9% дисперсии и интерпретируется как уровень развития материального производства в регионе, определяющий, в свою очередь, уровень показателей доходов городского населения региона.

Вторая главная компонента обеспечивает 20,8% суммарной дисперсии и интерпретируется как концентрация промышленности в регионе, что определяется значительным влиянием таких показателей, как число предприятий и организаций (Х₅), стоимость основных фондов (Х₇) и инвестиции в основной капитал региона (Х₁₀).

Третья из выделенных компонент дает вклад 19,8% в описание дисперсии региональных параметров и интерпретируется как специализация региона и уровень развития сельского хозяйства, т.к. выражается сочетанием числа фермерских хозяйств в регионе (Х₉) и индексом физического объема продукции сельского хозяйства (Х₁₃).

Четвертая главная компонента обусловливает 17% дисперсии и интерпретируется как уровень развития торговли в регионе, поскольку в значительной мере определяется индексом физического объема розничной торговли в регионе (Х₁₄).

Для Западно-Сибирского экономического района вклад каждой из выделенных четырех главных компонент в суммарную дисперсию региональных параметров соответственно составляет – 42,2%; 21,1%; 14,9% и 13,5%, что в сумме дает 91,7%.

Первая компонента во многом определяется концентрацией производственного капитала в регионе и высокими показателями его эффективного использования, что обусловливает высокие показатели доходов населения.

Вторая главная компонента характеризуется отраслевой специализацией региона и ее влиянием на долю городского населения (ниже средней по России) и высоким уровнем безработицы в регионе (Х₄).

Третья компонента выражает высокий уровень доходов населения региона, поскольку он в значительной степени обусловлен большим приростом по вкладам населения в банках (Х₂₁).

Четвертая главная компонента интерпретируется как уровень развития сельского хозяйства в регионе, что определяется такими тесно взаимосвязанными показателями, как число фермерских хозяйств в регионе (Х₉) и индекс физического объема продукции сельского хозяйства (Х₁₃).

Для Восточно-Сибирского экономического района было выделено три главные компоненты, вклад которых в суммарную дисперсию соответственно составляет 51,3%; 26,4% и 15,4%, что в сумме дает 93,1%.

Первая главная компонента интерпретируется как концентрация производственного и финансового капитала в регионе и эффективность его функционирования, поскольку определяется тесной связью показателей ресурсной обеспеченности с показателями результативности.

Вторая главная компонента характеризует специализацию региона и уровень развития сферы услуг, что обусловлено выделением таких показателей, как объем бытовых услуг (Х₁₆) и объем платных услуг (Х₁₇) в регионе. Специализация (Х₆), в свою очередь, определяет высокий уровень безработицы в регионе (Х₄).

Третья компонента интерпретируется как уровень развития материального производства, т.к. выделяются значения таких показателей как индексы физического объема промышленности (Х₁₂) и объема продукции сельского хозяйства (Х₁₃).

Для Дальневосточного экономического района компонентный анализ выделил четыре главные компоненты, общий вклад которых в суммарную дисперсию региональных параметров составил 80,3%.

Первая главная компонента интерпретируется как структура населения региона, определяющая уровень его доходов, что выражается взаимосвязью группы социально-демографических показателей с показателями доходов населения. Вклад первой компоненты в суммарную дисперсию обеспечивает 26,4%.

Вторая главная компонента интерпретируется как концентрация производственного капитала в регионе, поскольку она выражает взаимосвязь показателей ресурсной обеспеченности: число предприятий и организаций в регионе (Х₅), стоимость основных фондов (Х₇), число фермерских хозяйств (Х₉) и инвестиции в основной капитал (Х₁₀). Вклад второй компоненты составляет 23,6% дисперсии региональных параметров.

Третья компонента выражает уровень развития сферы услуг и торговли, что в большой степени обусловлено значением розничного товарооборота на душу населения региона, ее вклад в описание дисперсии параметров составляет 17,5%.

Четвертая главная компонента определяет уровень безработицы в регионе (Х₄), поскольку обусловлена значением именно этого показателя, вклад четвертой компоненты в общую дисперсию равен 12,8%.

Анализ полученных результатов показывает, что практически во всех экономических районах, для которых проводился компонентный анализ, первая и вторая главные компоненты формируются либо на базе параметров ресурсной обеспеченности региона, либо параметров результативности. Именно показатели этих групп региональных факторов обеспечивают максимальный вклад в суммарную дисперсию параметров.

Для экономических районов наиболее распространенными главными компонентами, выделенными на основе взаимосвязи региональных параметров, можно назвать следующие:

-  концентрация производственного и финансового капитала в регионе;

-  уровень развития материального производства;

-  специализация региона;

-  структура населения региона;

-  уровень развития сельского хозяйства;

-  уровень развития торговли и сферы услуг;

-  уровень показателей доходов населения.

Концентрация производственного и финансового капитала в регионе в виде первой, второй или третьей компоненты выделялась в каждом из анализируемых экономических районов. Весомое значение во взаимосвязи системы региональных показателей при выделении данной компоненты играет стоимость основных фондов в регионе. 

Уровень развития материального производства, характеризующий эффективность функционирования предприятий и организаций в регионе, в большей мере обеспечивается значениями валового регионального продукта на душу населения региона. Данная компонента выделялась в пяти экономических районах.

В четырех районах выделялась компонента, интерпретируемая как структура населения региона, в большей мере определяемая показателями долей городского мужского населения региона. Также специализация региона была выделена по четырем экономическим районам.

Остальные главные компоненты встречаются реже, а некоторые носят единичный характер и отражают определенную специфику региона. Так, по Центральному району четвертая компонента интерпретируется как уровень образования в регионе и больше ни в каких районах отдельно не выделяется.

Метод главных компонент оказывается весьма ценным инструментом территориальных исследований, поскольку дает возможность выявить и типичные сочетания некоторых региональных параметров, характерных для большинства субъектов РФ, и особенности, присущие лишь немногим регионам. В собственных значениях выделенных главных компонент наиболее весомыми оказались такие параметры, как стоимость основных фондов и валовой региональный продукт на душу населения, что определяет возможность типологической группировки регионов по величине среднедушевых денежных доходов населения и значениям выбранных параметров.

Типология по своей сути представляет классификационную, концептуальную схему расположения регионов относительно выделяемых признаков. При этом реальное разнообразие регионов, определяемое территориальной дифференциацией, сводится к небольшому числу групп. Название каждой группы регионов должно отражать определенный тип развития изучаемого явления. 

Предыдущая

Оглавление

Следующая