6.6. Математический инструментарий принятия решения

Этот инструментарий (экономико-математические модели и методы - ЭМММ) представляет собой логический системный подход к решению проблемы управления. Схематически его можно изобразить, как это показано на рис. 27.

С точки зрения ЭМММ центральным моментом становится конструирование модели - абстрактного представления существующей проблемной ситуации. Обычно такая модель представляется в виде математического соотношения или графика.

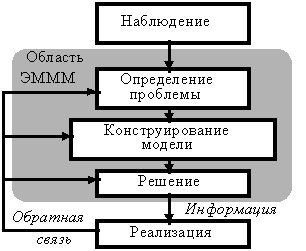
Рис. 27. Использование ЭМММ при принятии решения

Предположим, фирма продает продукт по цене 20$, а его себестоимость - 5$. Полная прибыль

z = 20x-5x,

где x - число проданных единиц продукта, x и z - переменные, причем x - независимая, z - зависимая переменная; числа 20 и 5 - параметры.

Это соотношение - модель определения прибыли фирмы. Предположим, что продукт делается из стали и что фирма имеет 100 кг стали в своем распоряжении. На единицу продукта идет 4 кг стали. Следовательно, 4x = 100 кг.

Теперь модель выглядит так:

z = 20x - 5x. (1)

4x = 100. (2)

Здесь уравнение (1) - целевая функция, а уравнение ресурсов (2) - ограничение, то есть управленческое решение будет моделироваться так:

max z = 20x - 5x при 4x = 100.

Итак, если менеджер решает продать 25 единиц продукта (x = 25), фирма получит прибыль z = 375$. Заметим, что эта величина не действительное решение, а скорее информация, которая служит рекомендацией или руководством, помогающим менеджеру принять решение.

Некоторые модели не дают ответа и рекомендаций по решению. Однако они обеспечивают описательные результаты: эти результаты описывают моделируемую систему (например, дисперсия продаж некоторых товаров по месяцам в течение года).

Менеджер не прямо применяет полученный результат как решение, а сопоставляет его со своими оценками и прогнозами. Если менеджер не использует результаты ЭМММ, то они нереализуемы. Если это так, то должны быть введены дополнительные ресурсы или усилия при решении проблемы, конструировании модели и ее решении.

Результаты моделирования и решения основаны на сравнении путем обратной связи с первоначальной моделью, которая может модифицироваться при испытаниях в различных условиях и будущих решениях менеджера. Результаты могут указывать, что проблема полностью не охвачена ранее и это требует изменений или реконструкции первоначальной модели. В этом случае ЭМММ представляют непрерывный процесс, а не одиночное решение одиночной проблемы.

Классификация ЭМММ приведена на рис. 28. В курсе ЭМММ подробно рассматривается большая часть этих процедур. Здесь далее содержится краткая оценка их практической применимости в современном менеджменте.

Наиболее популярна техника линейного программирования. К ней проводят задачи, связанные с ограничениями (по ресурсам, времени, рабочей силе, энергии, финансам, материалам) и с целевой функцией типа максимизации прибыли. Существенным является линейность функциональных соотношений в математической модели. Конкретная техника решений состоит в использовании алгоритма последовательных шагов (т. е. программы).

При использовании вероятностных процедур, в отличие от линейного программирования, результаты носят вероятностный характер и должны содержать некоторую неопределенность и возможность присутствия альтернативных решений.

Процедуры управления запасами специально разработаны для анализа проблем запасов, что характерно для большинства коммерческих фирм. Эта частная функция управления вносит существенный вклад в издержки любого бизнеса.

Сетевые модели скорее более диаграммы, чем точные математические соотношения. Они представляют в наглядной форме систему действий для их анализа.

Другие процедуры являются многоступенчатыми (программными), но отличными по постановке от линейной задачи.

В США по состоянию на 1980 г. в учебных заведениях, правительственных учреждениях, бизнесе и промышленности частота использования процедур характеризуется данными табл. 6.3.

Рис. 28. Классификация ЭМММ

Таблица 6.3

Частота использования и относительная важность процедур

Процедура	% пользователей	Ранг полезности	Общий ранг	Место по важности
Линейное программирование	83,8	2	2,4	2
Имитационные модели	80,3	1	1,25	1
Сетевые модели	58,1	4	6,9	4
Теория очередей	54,7	7	12,7	5
Дерево решений	54,7	3	5,5	3
Анализ замещений	38,5	5	13,0	6
Интегральное программир.	38,5	6	15,6	7
Динамическое программир.	32,5	11	38,8	10
Марковские процессы	31,6	10	31,6	9
Нелинейное программир.	30,7	9	29	8
Программированные результаты	20,5	8	39	11
Теория игр	13,7	12	88	12

Итак, мы видим, что в практическом менеджменте наибольшее значение придается:
- имитационным моделям,
- линейному программированию,
- графам (деревьям) решений,
- сетевым моделям,
- теории очередей (задачам массового обслуживания),
- анализу замещения,
- интегральному программированию.

Частота использования различных методов респондентами отражена в табл. 6.4.

Таблица 6.4

Доля респондентов, использующих конкретные методы

Сфера управления	% респондентов
Статистический анализ	98,4
Имитация на компьютерах	87,1
Сетевые методы	74,1
Линейное программирование	74,2
Теория очередей	59,7
Нелинейное программирование	46,8
Динамическое программирование	38,7
Теория игр	30,6

Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности изменений продукции, нерегулярности производства, внутренних дестабилизирующих факторов, нерегулярности снабжения, финансирования, сбыта и т.д.

Большинство этих факторов носит нестационарный характер, что фактически исключает возможность использования эконометрических моделей в планировании и управлении реальным производством.

Оглавление