Глава 3. Статистика нечисловых данных конкретных видов

3.4. Теория люсианов

          Асимптотика растущей размерности и проверяемые гипотезы. Продолжим изучение модели порождения данных (6) - (7) раздела 3.2. Будем использовать асимптотику s = const, k → ∞. При этом число неизвестных параметров растет пропорционально объему данных.

          В последние десятилетия (с начала 1970-х годов) в прикладной статистике все большее распространение получают постановки, в которых число неизвестных параметров растет вместе с объемом выборки. Результаты, полученные в подобных постановках, называют найденными «в асимптотике растущей размерности» или «в асимптотике А.Н.Колмогорова» [13], перенося терминологию исследований по дискриминантному анализу на общий случай. Как известно, в задаче дискриминации в две совокупности (т.е. отнесения вновь появляющегося объекта к одному из двух классов) академик АН СССР А.Н. Колмогоров (1903 - 1987) предложил рассматривать асимптотику

,

где А - размерность пространства (число признаков), N_i - объемы обучающих выборок, λ_i - константы, i = 1,2. Эта асимптотика естественна при обработке многих видов технических, организационно-экономических, социологических, медицинских данных, поскольку число признаков, определяемых для каждого изучаемого объекта, респондента или пациента, обычно имеет тот же порядок, что и объем выборки.

          Пусть A₁, A₂, ..., A_s - независимые (между собой) люсианы с векторами параметров Р₁, Р₂, ..., Р_s соответственно. Гипотезой согласованности будем называть гипотезу

Р₁ = Р₂ = ...= Р_s.            (1)

Для ранжировок и разбиений под согласованностью понимают более частную гипотезу, предполагающую отрицание равномерности распределений (т.е. одинаковой вероятности появления каждой возможной ранжировки или разбиения), что соответствует замене проверки гипотезы (1) на проверку гипотезы

Р₁ = Р₂ = ...= Р_s = (1/2, 1/2, ..., 1/2).            (2)

Как разъяснено в [1, 14], гипотеза (1) более адекватна конкретным задачам обработки реальных данных, например, экспертных оценок, чем (2). Поэтому полученные от экспертов данные, содержащие противоречия, целесообразно рассматривать как люсианы и проверять гипотезу (1), а не подбирать ближайшие ранжировки или разбиения , после чего проверять согласованность методами теории случайных ранжировок или разбиений, как иногда рекомендуется.

          Пусть A₁, A₂, ..., A_m и B₁, B₂, ..., B_n - независимые в совокупности люсианы длины k, одинаково распределенные в каждой группе с параметрами Р(А) и Р(В) соответственно. Гипотезой однородности называется гипотеза

Р(А) = Р(В).

В асимптотике растущей размерности принимаем, что m и n постоянны, а k → ∞.

          Пусть (A_i, B_i), i = 1. 2, ..., s - последовательность (фиксированной длины) пар люсианов. Пары предполагаются независимыми между собой. Требуется проверить гипотезу независимости A_i и B_i, т.е. внутри пар. В ранее введенных обозначениях гипотеза независимости - это гипотеза

P(X_ij(A) = 1, X_ij(B) = 1) = P(X_ij(A) = 1)P(X_ij(B) = 1),

 i = 1, 2, ..., s; j = 1, 2, ..., k,

проверяемая в предположении

Р₁(А) = Р₂(А) = ... = Р_s(А), Р₁(B) = Р₂(B) = ... = Р_s(B).

          В настоящем разделе излагается метод проверки гипотез о люсианах в асимптотике растущей размерности на примере гипотезы согласованности. Эти результаты получены в [1, 14, 15]. Дальнейшее изучение проведено Г.В. Рыдановой, Т.Н. Дылько, Г.В. Раушенбахом, О.В. Филипповым, А.М. Никифоровым и др. Гипотеза однородности рассмотрена, например, в [15]. Методы проверки гипотезы однородности люсианов развиты и изучены Г.В. Рыдановой [16] на основе описанного ниже подхода. Она помимо доказательства предельных теорем провела подробное изучение скорости сходимости методом статистических испытаний.

          Методы проверки согласованности люсианов нашли практическое применение, в частности, в медицине. Они были использованы в кардиологии при анализе данных кинетотопографии [15, 17, 18]. Эти методы включены в методические рекомендации Академии медицинских наук СССР и Ученого Медицинского Совета Минздрава СССР по управлению научными медицинскими исследованиями [19].

          Метод проверки гипотез о люсианах в асимптотике растущей размерности. Будем использовать дальнейшее развитие метода, описанного в предыдущем разделе 3.3. Почему нельзя использовать иные подходы, имеющиеся в математической статистике? Поскольку число неизвестных параметров растет вместе с объемом выборки и пропорционально ему, эти параметры не являются мешающими (в том смысле, как этот термин понимается в теории математической статистики). Отметим, что согласно [20] равномерно наиболее мощных критериев не существует, поскольку параметров много. Не останавливаясь на других подходах математической статистики, констатируем необходимость применения метода проверки гипотез по совокупности малых выборок.

          Пусть имеются k выборок, независимых между собой. Пусть при справедливости нулевой гипотезы по каждой из выборок можно построить несмещенную оценку  векторного нуля , где р > 1, i = 1, 2, ..., k. Другими словами, пусть распределение i-ой выборки описывается параметром θ_i, лежащим в произвольном пространстве, а нулевая гипотеза, очевидно, состоит в том, что θ_iΘ_0i, где Θ_0i - собственное подмножество множества {θ_i}. Предполагается, что можно по i-ой выборке вычислить статистику ξ_i такую, что

Mξ_i = 0                 (3)

при всех θ_iΘ_0i. Очевидно, ξ_i ≡ 0 удовлетворяют (1). Однако для рассматриваемого метода необходимо, чтобы при всех θ_iΘ_0i ковариационная матрица вектора ξ_i была ненулевой:

.                 (4)

          В теории математической статистики иногда используют понятие полноты параметрического семейства распределений. Если рассматриваемое семейство является полным - а так и есть для люсианов, - то не существует достаточной статистики, удовлетворяющей одновременно условиям (1) и (2) (см., например, [21, §§2.12-2.14]). Поэтому будем использовать статистики, не являющиеся достаточными.

          Следующее предположение - ковариационные матрицы статистик ξ_i, т.е. Cov(ξ_i), также допускают несмещенные оценки S_i по тем же выборкам:

M(S_i) = Cov(ξ_i)               (5)

при всех θ_iΘ_0i.

          Рассматриваемый метод основан на том, что поскольку случайные вектора ξ_i определяются по независимым между собой выборкам, то ξ_i независимы в совокупности, а потому случайный вектор

                 (6)

является суммой независимых случайных векторов, имеет в силу (3) нулевое математическое ожидание, а его ковариационная матрица равна

.

При справедливости многомерной центральной предельной теоремы (простейшее условие справедливости этой теоремы для ξ_i в случае люсианов - отделенность от 0 и 1 всех элементов матриц P_j, равномерная по s и k) вектор ξ является асимптотически нормальным, т.е. при k → ∞ распределение ξ сближается (в смысле, раскрытом в приложении 1) с многомерным нормальным распределением N(0; C_k).

          Однако эту сходимость нельзя непосредственно использовать для проверки исходной гипотезы, поскольку матрица C_k неизвестна статистику. Необходимо оценить эту матрицу по статистическим данным. В силу (5) в качестве оценки C_k естественно использовать

.

Простейшая формулировка условий справедливости такой замены - предположение о том, что к последовательности S_i можно применить закон больших чисел. А именно, пусть существует неотрицательно определенная матрица С такая, что при k → ∞

.                  (7)

В силу результатов приложения 1 из асимптотической нормальности ξ и соотношений (7) следует, что распределение статистики

сходится к нормальному распределению N(0; C). При этом, если некоторый случайный вектор τ имеет распределение N(0; C), то распределение случайной величины q(η) сходится к распределению q(τ) для произвольной интегрируемой по Риману по любому кубу функции q: R^p → R¹. Для проверки нулевой гипотезы предлагается пользоваться статистикой q(η) при подходящей функции q, а процентные точки брать соответственно распределению q(τ). В этом и состоит рассматриваемый метод проверки гипотез о люсианах в асимптотике растущей размерности. Для реальных расчетов целесообразно использовать линейные или квадратические функции q от координат вектора η.

          Отклонения от нулевой гипотезы приводят, как правило, к нарушению равенств (3) и (4). Случайный вектор η при этом обычно остается асимптотически нормальным, но с другими параметрами, что может быть обычным образом использовано для построения оптимального решающего правила, соответствующего заданной альтернативе (например, согласно лемме Неймана-Пирсона). Поведение при альтернативах для некоторых гипотез изучено в [15, 16], здесь его не будем рассматривать, поскольку вычисление мощности не требует новых идей.

          Несмещенные оценки параметров асимптотического распределения вектора попарных расстояний. Применим описанный выше метод для проверки гипотезы согласованности люсианов. Исходные данные - люсианы

A_j = (X_1j, X_2j, ..., X_kj), j = 1, 2, ..., s.

В качестве i-й выборки возьмем совокупность испытаний Бернулли, стоящих на i-м месте в рассматриваемых люсианах: 

X_i1, X_i2, ..., X_is.                (8)

При справедливости нулевой гипотезы в (8) стоят независимые испытания Бернулли с одной и той же вероятностью успеха p_i; при нарушении нулевой гипотезы согласованности независимость испытаний Бернулли сохраняется, но вероятности успеха могут различаться.

          В качестве вектора ξ, на основе которого строятся статистики для проверки согласованности, будем использовать вектор попарных расстояний между люсианами

ξ = {d(A_p, A_q), 1 < p < q < s},            (9)

в котором пары (p, q) упорядочены лексикографически,

.       (10)

В главе 1 это расстояние выведено из некоторой системы аксиом (напомним, что совокупность векторов из 0 и 1 размерности k находится во взаимнооднозначном соответствии с совокупностью подмножеств множества из k элементов; при этом 1 соответствует тому, что элемент входит в подмножество, а 0 - что не входит).

          Из вида расстояния в формуле (10) следует, что введенный в (9) вектор ξ имеет вид (6) с

ξ_i = μ_i{|X_ip - X_iq|, 1 < p < q < s}.         (11)

Следовательно, для применения описанного выше метода проверки гипотез о люсианах в асимптотике растущей размерности достаточно построить на основе вектора ξ_i из (11) несмещенную оценку 0 и найти несмещенную оценку ковариационной матрицы этой оценки.

          Чтобы применить общую схему, необходимо начать с построения статистики β такой, чтобы при всех p_i имело место равенство

M(|X_ip - X_iq| - β) - 0,  1 < p < q < s.

Элементарный расчет дает:

M|X_ip - X_iq| = 2p_i (1 - p_i).

          Как известно [22, с.56-57], несмещенная оценка многочлена

по результатам m независимых испытаний Бернулли с вероятностью успеха р в каждом имеет вид

,             (12)

где γ - общее число успехов в m испытаниях и использовано обозначение

n^[h] = n(n - 1)...(n - h + 1).

Ясно, что многочлены степени m + 1 и более высокой невозможно несмещенно оценить по результатам m испытаний.

          В случае f(p) = 2p(1 - p) в соответствии с (12) получаем несмещенную оценку

.             (13)

          Таким образом, можно применять общий метод проверки гипотез о люсианах в асимптотике растущей размерности с

ξ_i = μ_i ({|X_ip - X_iq|, 1 < p < q < s} - β_ie),

где коэффициенты β_i определяются с помощью формулы (13) по γ_i - общему числу единиц, стоящих на i-м месте в люсианах A₁, A₂, ..., A_s, а  e - вектор размерности s(s - 1)/2 с единичными координатами. Тогда несмещенная оценка 0, о которой идет речь в методе проверки гипотез по совокупности малых выборок, имеет вид

.

          Для использования статистики типа η, распределение которой приближается с помощью нормального распределения

,

необходимо уметь несмещенно оценивать ковариационные матрицы Cov(ξ_i). Для этого достаточно найти математические ожидания элементов матрицы  как функции (многочлены) от p_i, а затем использовать формулу (12) для получения несмещенных оценок.

          Вычисление матрицы  хотя и трудоемко, но не содержит каких-либо принципиальных трудностей. В [15] вычислены диагональные элементы рассматриваемой матрицы. Вычисление занимает около 2,5 книжных страниц (с.299-301). Поэтому здесь приведен только окончательный итог.

          Обозначим для краткости p_i = р. В [15] показано, что

.

Если двухэлементные множества {p, q} и {r, t} не имеют ни одного общего элемента, то

,

а если имеют ровно один общий элемент, то

.

          С помощью формулы (12) получаем несмещенные оценки для D, C₁ и C₂ как многочленов от р:

,

,

.

С помощью трех чисел  выписывается несмещенная оценка матрицы ковариаций вектора ξ_i/μ_i, которую обозначим B_i. Тогда асимптотически нормальный вектор ξ имеет нулевое математическое ожидание и ковариационную матрицу, несмещенно и состоятельно (в смысле соотношений (7)) оцениваемую с помощью

.             (14)

          Асимптотическая нормальность доказывается, естественно, в схеме серий. Достаточным условием является существование положительной константы ε такой, что

              (15)

при всех k и i, 1 < i < k.

          Поскольку D, C₁ и C₂ являются многочленами четвертой степени от р, то несмещенные оценки для них существуют при s > 4. Если же s < 4, то несмещенных оценок не существует. Поэтому указанным методом проверять согласованность можно лишь при числе люсианов s > 4.

          Проверка согласованности люсианов. Пусть α - нормально распределенный случайный вектор размерности s(s - 1)/2 с нулевым математическим ожиданием и ковариационной матрицей, определенной формулой (14). Согласно результатам приложения 1 для любой действительнозначной функции f, интегрируемой по Риману по любому гиперкубу, распределения случайных величин f(ξ) и f(α) сближаются при k → ∞. Это означает, что вместо распределения случайной величины f(ξ) для построения критериев проверки гипотез можно использовать распределение случайной величины f(α). Более того, аналогичный результат верен при замене f на f_n (при слабых внутриматематических условиях регулярности, наложенных на последовательность функций f_n). Следовательно, для проверки гипотезы согласованности люсианов можно пользоваться любой статистикой f_n(ξ), для которой могут быть вычислены на ЭВМ или заранее табулированы процентные точки распределения f_n(α), аппроксимирующего распределение f_n(ξ).

          В частности, можно использовать линейные статистики, представляющие собой скалярное произведение случайного вектора ξ и некоторого заданного детерминированного вектора коэффициентов а, т.е.

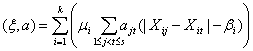.                (16)

Линейные статистики имеют нулевое математическое ожидание и дисперсию, очевидным образом выражающуюся через матрицу коэффициентов ||a_ij|| и числа D, C₁ и C₂, а потому несмещенно и состоятельно оцениваемую с помощью с помощью выписанных выше оценок для D, C₁ и C₂.

          Отметим, что (ξ, а) = 0 при a_ij ≡ 1, 1 < j < t < s. Это следует как из непосредственного вычисления дисперсии (ξ, а), так и из того, что (ξ, а) в рассматриваемом случае выражается через достаточную статистику (γ₁, γ₂, ..., γ_k) и является несмещенной оценкой нуля, а семейство биномиальных распределений полно, т.е. существует только одна несмещенная оценка нуля - тождественный нуль. Таким образом, сумма координат вектора ξ, т.е. непосредственный аналог коэффициента ранговой конкордации Кендалла-Смита из теории ранговой корреляции, тождественно равна 0.

          Распределение статистики (16) при альтернативах изучено в работе [16].

          Рассмотрим два частных случая.

          Первый частный случай. Проверка согласованности двух определенных люсианов (ответов двух экспертов), j-го и t-го, может осуществляться с помощью статистики (16), в которой отличен от 0 только член с a_jt = 1. Оценкой дисперсии является D*.

          Второй частный случай. Пусть необходимо проверить согласованность люсианов с одним из них, скажем, с j-м (например, люсианы отражают мнения экспертов, а j-й из них является наиболее компетентным - по априорной оценке, или «лицом, принимающим решения», или его мнение сильно отличается от мнений остальных). Это можно сделать с помощью статистики (16), в которой

a_jt = 1, t -= j + 1, j + 2, ..., s;   a_tj = 1, t = 1, 2, ..., j - 1;

a_qt =0, q ≠ j, t ≠ j, 1 < q < t < s.

Другими словами, она имеет вид

,              (17)

где расстояние d между люсианами определено в (10), а β_i  - в (13) с заменой m на s и γ на γ_i. Используя полученные ранее несмещенные оценки элементов ковариационной матрицы, нетрудно показать, что несмещенная и состоятельная (в смысле формулы (7) выше) оценка дисперсии W имеет вид

.

Тогда при выполнении некоторых внутриматематических условий регулярности, например, условий (15), распределение статистики

сходится при k → ∞, s = const к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1 (при справедливости гипотезы (1) согласованности люсианов).

          Статистика (17) наряду со статистикой, предназначенной для проверки гипотезы однородности люсианов, включена в «Методические рекомендации» АМН СССР и УМС Минздрава СССР [19]. Последнюю статистику не расписываем здесь, поскольку для этого не требуются новые идеи.

          Различные подходы к понятию согласованности. Обсудим условия, при выполнении которых люсианы естественно считать согласованными (а экспертов, чьи мнения отражают люсианы, имеющими единое мнение, искаженное случайными ошибками), т.е. обсудим различные методы проверки гипотезы (1).

          Полное индивидуальное согласие имеет место, если никакие два эксперта не являются «несогласованными». Уровень значимости определяется описанным выше способом (первый частный случай). Однако наличие одной или нескольких пар экспертов, чьи мнения нельзя считать согласованными, не свидетельствует о необходимости отклонения гипотезы (1), поскольку парных проверок проводится много, а именно, s(s - 1) > 6, а способы установления уровня значимости при множественных проверках, зависимых между собой, к настоящему времени плохо разработаны [5? раздел 11.1]. Проблема множественных проверок для количественных признаков обсуждается А.А. Любищевым [23, с.36-39], выход дается дисперсионным анализом. Можно брать не все попарные проверки, а только для [s/2] пар люсианов, причем разбиение на пары проводить независимо от принятых люсианами значений, как это делает Т.Н. Дылько [24]. Тогда для проверки гипотезы (1) на уровне значимости α надо брать для проверки в каждой паре уровень значимости β, где β рассчитывается понятным образом, приближенно β = α / [s/2].

          Полное согласие в целом означает, что для любого эксперта мнения всех остальных оказываются с ним согласованными при использовании статистики (17) (второй частный случай). Отсутствие подобного согласия для одного или нескольких экспертов не означает отклонения гипотезы согласованности люсианов (1) - по тем же причинам, что и в предыдущем случае.

          Минимальное согласие имеют мнения экспертов, когда хотя бы для одного из них гипотеза согласованности не отвергается с помощью статистики (17). В этом случае групповое мнение целесообразно строить, выделяя «ядро», о чем подробнее сказано ниже.

          Расстояние d между люсианами (см. формулу (10)) введено аксиоматически в главе 1 (напомним, что реализацию люсиана можно рассматривать как подмножество конечного множества). Там же из иной системы аксиом выведено другое расстояние - D-метрика. Рассмотрим проверку согласованности люсианов с использованием D-метрики. В этом случае расстояние между люсианами А₁ и А₂ имеет вид

где

.

Ясно, что теория, основанная на D-метрике, из-за наличия знаменателя в только что приведенной формуле существенно сложнее теории, основанной на метрике d. Ясно, что описанный выше метод проверки гипотез о люсианах в асимптотике растущей размерности применить не удается. Чтобы продемонстрировать существенное усложнение ситуации, опишем лишь асимптотическое поведение расстояния D(А₁, А₂) между двумя люсианами.

          Теорема [25]. Пусть p_1i и p_2i отделены от 0 и 1, а μ_i отделены от 0 и +∞. Тогда расстояние D(А₁, А₂) между люсианами А₁ и А₂ асимптотически нормально при k → ∞ с параметрами

,

т.е. для любого числа х справедливо предельное соотношение

,

где Φ(х) - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

          Величины N_j, j = 1, 2, 2, 4, 5, выражаются через μ_i и величины 

p_3i = p_1i + p_2i - 2p_1i p_2i, p_4i = p_1i + p_2i - p_1i p_2i    

следующим образом:

.

          Следствие 1. Пусть p_1i = p₁ и p_2i = p₂ при всех i, k, причем p₁ и p₂ лежат внутри отрезка (0; 1). Пусть μ_i отделены от 0 и +∞. Тогда расстояние D(А₁, А₂) между люсианами А₁ и А₂ асимптотически нормально при k → ∞ с параметрами

,

где

p₃ = p₁ + p₂ - 2p₁p₂,   p₄ = p₁ + p₂ - p₁p₂.  

          Следствие 2. Пусть в предположениях следствия 1 p₁ = p₂ = р и μ_i = 1 при всех i, k. Тогда

.

          Замечание. Пусть в следствии 2 р = 1/2. Тогда А₁ и А₂ - люсианы, равномерно распределенные на множестве всех последовательностей из 0 и 1 длины k. В частности, эти люсианы могут соответствовать независимым случайным множествам, равномерно распределенным на совокупности всех подмножеств конечного множества из k элементов, или независимым толерантностям, равномерно распределенным на множестве всех толерантностей, определенных на множества из m элементов, где m(m - 1)/2 = k. По следствию 2 расстояние между люсианами D(А₁, А₂) асимптотически нормально с математическим ожиданием 0,667 и дисперсией 0,296 k^-1. Напомним, что распределения коэффициентов ранговой корреляции Кендалла и Спирмена изучены (в основном) лишь при условии равномерности распределения случайных ранжировок на множестве всех возможных ранжировок фиксированного числа объектов. Для теории люсианов случай равномерности распределения - весьма частный, а для теории ранжировок - основной. Как уже говорилось, отказ от равномерности - привлекательная черта теории люсианов. 

          Классификация люсианов. Отсутствие согласованности в одном из перечисленных выше смыслов позволяет сделать заключение о целесообразности разбиения всех люсианов (например, если они выражают мнения экспертов) на группы близких между собой, т.е. о целесообразности классификации люсианов, точнее, их кластер-анализа. Поскольку введена мера близости между люсианами d(А₁, А₂) или D(А₁, А₂), то напрашивается следующий способ действий: провести разбиение на кластеры с помощью одного из алгоритмов, основанных на использовании меры близости, а затем проверить мнения в каждом классе на согласованность. Однако применение того или иного алгоритма кластер-анализа, вообще говоря, может нарушить предпосылки описанных выше способов описанных выше способов проверки согласованности (ср. обсуждение похожей проблемы, связанной с применением регрессионного анализа после кластер-анализа, в [5, гл.11]). Поэтому опишем методы классификации, опирающиеся на результаты проверки согласованности.

          Разбиение на кластеры, внутри каждого из которых имеет место «полное индивидуальное согласие», может быть проведено с помощью агломеративного иерархического алгоритма «дальнего соседа», дополненного ограничением сверху на диаметр кластера. Это ограничение строится из статистических соображений, в отличие от методов, обычно используемых в кластер-анализе [5, гл.5]. При этом в качестве меры близости между люсианами используют не расстояния d или D, а модуль статистики, применяемой для проверки согласованности двух люсианов, т.е. статистики (16), в которой только одно из чисел a_ij отлично от 0. Упомянутое ограничение таково: диаметр кластера не должен превосходить процентной точки предельного распределения, соответствующей используемому при анализе рассматриваемых данных уровню значимости (можно порекомендовать 5%-й уровень значимости). В результате работы алгоритма получим кластеры, в которых имеется «полное индивидуальное согласие», причем объединение любых двух кластеров приведет к исчезновению этого свойства у объединения. Поскольку способ выделения итогового разбиения из иерархического дерева разбиений имеет вероятностно-статистическое обоснование, изложенное выше, то описанный метод классификации люсианов следует считать - в терминологии [26] - не методом анализа данных, а вероятностно-статистическим методом.

          Кластеры «с полным согласием в целом» могут быть получены с помощью агломеративного иерархического алгоритма, в котором мерой близости двух кластеров является максимальное значение модуля статистики (17), когда j пробегает номера мнений (люсианов), вошедших в объединение рассматриваемых кластеров, а суммирование в (17) проводится по всем люсианам в этом объединении. Ограничение сверху на меру близости кластеров определяется процентной точкой предельного распределения статистики W, заданной формулой (17).

          Кластеры «с минимальным согласием» можно получить, при фиксированном j выделяя совокупность люсианов, согласованных с A_j в смысле статистики W из (17).

          На основе двух рассмотренных выше частных случаев линейной статистики (16) можно строить и другие способы классификации. Например, для каждого люсиана A_m можно выделить кластер «типа шара» (см. [5, гл.5]) из люсианов, попарно согласованных с A_m. Все такие способы имеют вероятностно-статистическое обоснование, и потому к ним относится сказанное выше относительно выделения кластеров «с полным индивидуальным согласием».

          Замечание. Проверка согласованности приведенными выше критериями может привести к отрицательному результату двумя способами - либо значение статистики окажется слишком большим, либо слишком малым. Первое означает, что гипотеза согласованности люсианов (1) неверна, вторая - что неверна вероятностная модель реального явления или процесса, основанная на люсианах. С необходимостью учета второй возможности мы столкнулись при применении теории люсианов для анализа данных топокарт, полученных при проведении кинетокардиографии у больных инфарктом миокарда [17, 18].

          Нахождение среднего. В результате классификации получаем согласованные (в одном из указанных выше смыслов) группы люсианов. Для каждой из них полезно рассмотреть среднее. В зависимости от конкретных приложений в прикладных исследованиях применяют либо среднее в виде последовательностей 0 и 1, т.е. в виде реализации люсиана, либо среднее в виде последовательности оценок вероятностей (p₁^, p₂, ..., p_k). Кроме того, оно может находиться либо с помощью методов, подавляющих «засорения» («выбросы»), либо без учета возможности засорения. Рассмотрим все четыре возможности.

          В соответствии с подходом главы 2 при отсутствии засорения эмпирическое среднее ищется как решение задачи

,            (18)

где A₁, A₂, ..., A_m - люсианы, входящие в рассматриваемый кластер, Х - множество, которому принадлежит среднее. Если Х - совокупность последовательностей из 0 и 1, то правило (18) дает решение по правилу большинства.  

          Если Х - пространство последовательностей вероятностей, то решением задачи (18) является та же последовательность 0 и 1, что и в первом случае. Поэтому в качестве среднего вместо решения задачи (18) целесообразно рассматривать просто последовательность частот.

          Асимптотическое поведение средних при m → ∞ вытекает из законов больших чисел, теорем, описывающих асимптотику решений экстремальных статистических задач (глава 2), и теоремы Муавра-Лапласа соответственно.

          В работе [27] при анализе результатов эксперимента показано, что ответы реальных экспертов разбиваются на многочисленное «ядро», расположенное вокруг истинного мнения, и отдельных «диссидентов», разбросанных по периферии. Причем оценка истинного мнения по «ядру» является более точной, чем по всей совокупности, поскольку мнения «диссидентов» не отражают истинного мнения. Поэтому для построения группового мнения, в том числе среднего для совокупности люсианов, отражающих мнения экспертов, естественно применять методы, подавляющие мнения «диссидентов», что соответствует методологии робастности.

          «Ядро» может быть построено следующим образом. Решается задача (18) с конечным множеством Х, состоящим из всех исходных люсианов: Х = {A₁, A₂, ..., A_m}, т.е. из результатов наблюдений выбирается тот, что находится «в центре» совокупности результатов наблюдений. Пусть A_j является решением этой задачи. В качестве ядра предлагается рассматривать совокупность всех люсианов, которые попарно согласованы с A_j. Другой вариант: рассматривается кластер с «полным внутренним согласием», куда входит A_j. (При этом, очевидно, должно быть изменено (уменьшено) критическое значение критерия по сравнению с процедурой, приведшей к выделению группы, нахождением группового мнения которой мы занимаемся.) Затем групповое мнение ищется лишь для элементов «ядра». Описанная процедура особенно необходима в случае, когда не было предварительного разбиения совокупности люсианов на группы согласованных друг с другом. Новым по сравнению с [27] является придание вероятностного смысла порогу, выделяющему «ядро».

          Обобщая идею выделения «ядра», приходим к «взвешенным итеративным методам оценивания среднего» (ВИМОП - оценкам среднего), введенным и изученным в работе [28]. Их применение для люсианов не требует специальных рассмотрений. 

          Таким образом, в настоящем разделе представлен ряд методов обработки специального вида объектов нечисловой природы - люсианов. При этом для решения одной и той же задачи, например, задачи классификации, предлагается ряд методов, точно так же, как для решения классической задачи проверки однородности двух независимых выборок имеется большое число методов [5, гл.4].