А.И.
Орлов
Теория принятия решений
Учебное пособие. - М.: Издательство "Март", 2004.
| Предыдущая |
2. ОПИСАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
2.3.7. Асимптотический линейный регрессионный анализ для интервальных данных
Перейдем к многомерному статистическому анализу. Сначала с позиций асимптотической математической статистики интервальных данных рассмотрим оценки метода наименьших квадратов (МНК).
Статистическое исследование зависимостей - одна из наиболее важных задач, которые возникают в различных областях науки и техники. Под словами "исследование зависимостей" имеется в виду выявление и описание существующей связи между исследуемыми переменными на основании результатов статистических наблюдений. К методам исследования зависимостей относятся регрессионный анализ, многомерное шкалирование, идентификация параметров динамических объектов, факторный анализ, дисперсионный анализ, корреляционный анализ и др. Однако многие реальные ситуации характеризуются наличием данных интервального типа, причем известны допустимые границы погрешностей (например, из технических паспортов средств измерения).
Если какая-либо группа объектов характеризуется переменными Х1, Х2, ,...,Хm и проведен эксперимент, состоящий из n опытов, где в каждом опыте эти переменные измеряются один раз, то экспериментатор получает набор чисел: Х1j, Х2j, ,...,Хmj (j = 1,…, n).
Однако процесс измерения, какой бы физической природы он ни был, обычно не дает однозначный результат. Реально результатом измерения какой-либо величины Х являются два числа: ХH— нижняя граница и ХB — верхняя граница. Причем ХИСТ Î [ХH, ХB], где ХИСТ - истинное значение измеряемой величины. Результат измерения можно записать как X: [ХH, ХB]. Интервальное число X может быть представлено другим способом, а именно, X: [Хm, Δx], где ХH = Хm - Δx , ХH = Хm + Δx . Здесь Хm - центр интервала (как правило, не совпадающий с ХИСТ), а Δx - максимально возможная погрешность измерения.
Метод наименьших квадратов для интервальных данных. Пусть математическая модель задана следующим образом:
у = Q(x,b) + ε,
где х = (х1 , х2,..., хm) - вектор влияющих переменных (факторов), поддающихся измерению; b = (b1 , b2 ,... , br ) - вектор оцениваемых параметров модели; у - отклик модели (скаляр); Q(x,b)- скалярная функция векторов х и b; наконец, ε - случайная ошибка (невязка, погрешность).
Пусть проведено n опытов, причем в каждом опыте измерены (один раз) значения отклика (у) и вектора факторов (х). Результаты измерений могут быть представлены в следующем виде:
Х = { хij ; i =1,n ; j = 1,m }, Y = (y1 , y2 ,…, yn ), Е = (ε1,ε2,…,εn),
где Х - матрица значений измеренного вектора (х) в n опытах; Y - вектор значений измеренного отклика в n опытах; Е - вектор случайных ошибок. Тогда выполняется матричное соотношение:
Y = Q(X,b) + Е ,
где Q(X,b) = (Q(x1 ,b), Q(x2 ,b), ..., Q(xn ,b))T, причем x1 , x2 , ..., xn - m-мерные вектора, которые составляют матрицу Х = (x1 , x2 , ..., xn )T.
Введем меру близости d(Y,Q) между векторами Y и Q. В МНК в качестве d(Y,Q) берется квадратичная форма взвешенных квадратов εi2 невязок εi = yi - Q(xi ,b), т.е.
d(Y,Q) = [ Y - Q(X,b)]T W[Y - Q(X,b)],
где W = {w ij , i, j =1,…, n} - матрица весов, не зависящая от b. Тогда в качестве оценки b можно выбрать такое b*, при котором мера близости d(Y,Q) принимает минимальное значение, т.е.
В общем случае решение этой экстремальной задачи может быть не единственным. Поэтому в дальнейшем будем иметь в виду одно из этих решений. Оно может быть выражено в виде b* = f(X,Y), где f(X,Y) = (f1(X,Y), f2(X,Y),..., fm(Х.У))T, причем fi(X,Y) непрерывны и дифференцируемы по (X,Y) Î Z, где Z -область определения функции f(X,Y). Эти свойства функции f(X,Y) дают возможность использовать подходы статистики интервальных данных.
Преимущество метода наименьших квадратов заключается в сравнительной простоте и универсальности вычислительных процедур. Однако не всегда оценка МНК является состоятельной (при функции Q(X,b), не являющейся линейной по векторному параметру b), что ограничивает его применение на практике.
Важным частным случаем является линейный МНК, когда Q(x,b) есть линейная функция от b:
у = bo xo+ b1 x1 + ... + bm xm + ε = b хT + ε ,
где, возможно, xo = 1, а bo - свободный член линейной комбинации. Как известно, в этом случае МНК-оценка имеет вид:
Если матрица XTWX не вырождена, то эта оценка является единственной. Если матрица весов W единичная, то
Пусть выполняются следующие предположения относительно распределения ошибок εi :
- ошибки εi имеют нулевые математические ожидания М{εi} = 0,
- результаты наблюдений имеют одинаковую дисперсию D { εi} = σ2,
- ошибки наблюдений некоррелированы, т.е. cov{ εi, εj} = 0.
Тогда, как известно, оценки МНК являются наилучшими линейными оценками, т.е. состоятельными и несмещенными оценками, которые представляют собой линейные функции результатов наблюдений и обладают минимальными дисперсиями среди множества всех линейных несмещенных оценок. Далее именно этот наиболее практически важный частный случай рассмотрим более подробно.
Как и в других постановках асимптотической математической статистики интервальных данных, при использовании МНК измеренные величины отличаются от истинных значений из-за наличия погрешностей измерения. Запишем истинные данные в следующей форме:
где R - индекс, указывающий на то, что значение истинное. Истинные и измеренные данные связаны следующим образом:
где 
Предположим, что
погрешности измерения отвечают граничным условиям
(48)
аналогичным ограничениям (1).
Пусть множество W возможных значений (XR ,YR) входит в Z -область определения функции f(X,Y). Рассмотрим b*R - оценку МНК, рассчитанную по истинным значениям факторов и отклика, и b* - оценку МНК, найденную по искаженным погрешностями данным. Тогда
Ввести понятие нотны придется несколько иначе, чем это было сделано выше, поскольку оценивается не одномерный параметр, а вектор. Положим:
Будем называть n(1) нижней нотной, а n(2) верхней нотной. Предположим, что при безграничном возрастании числа измерений n, т.е. при n→∞, вектора n(1), n(2) стремятся к постоянным значениям Ni(1), Ni(2) соответственно. Тогда Ni(1) будем называть нижней асимптотической нотной, а Ni(2) - верхней асимптотической нотной.
Рассмотрим доверительное множество Bα=Bα(n,b*R)
для вектора параметров b, т.е. замкнутое
связное множество точек в r-мерном евклидовом пространстве такое, что
где α
— доверительная вероятность, соответствующая Bα
(α ≈ 1). Другими словами, Bα (n, b*R) есть область
рассеивания (аналог эллипсоида рассеивания) случайного вектора b*R с доверительной вероятностью α и числом опытов n.
Из определения верхней и нижней нотн
следует, что всегда 
В соответствии
с определением нижней асимптотической нотны и верхней
асимптотической нотны можно считать, что 
при достаточно
большом числе наблюдений n. Этот многомерный интервал описывает r-мерный
гиперпараллелепипед P.
Каким-либо образом разобьем P на L гиперпараллелепипедов.
Пусть bk - внутренняя точка k-го
гиперпараллелепипеда. Учитывая свойства доверительного
множества и устремляя L к бесконечности, можно утверждать, что
где
Таким образом, множество C характеризует неопределенность при оценивании вектора параметров b. Его можно назвать доверительным множеством в статистике интервальных данных.
Введем некоторую меру М(X), характеризующую «величину»
множества X 
Rr По определению меры она удовлетворяет
условию: если 
и 
то M(X)=M(Z)+M(Y). Примерами такой меры являются площадь для r = 2 и объем для r = 3. Тогда:
М( C ) = М( P ) + М( F ), (49)
где F = C \ P. Здесь М(F) характеризует меру статистической неопределенности, в большинстве случаев она убывает при увеличении числа опытов n. В то же время М(P) характеризует меру интервальной (метрологической) неопределенности, и, как правило, М(P) стремится к некоторой постоянной величине при увеличении числа опытов n. Пусть теперь требуется найти то число опытов, при котором статистическая неопределенность составляет δ-ю часть общей неопределенности, т.е.
М( F ) = δ М( C ), (50)
где δ < 1. Тогда, подставив соотношение (50) в равенство (49) и решив уравнение относительно n, получим искомое число опытов. В асимптотической математической статистике интервальных данных оно называется "рациональным объемом выборки". При этом δ есть "степень малости" статистической неопределенности М(P) относительно всей неопределенности. Она выбирается из практических соображений. При использовании "принципа уравнивания погрешностей" согласно [3] имеем δ = 1/2.
Метод наименьших квадратов для линейной модели. Раccмотрим наиболее важный для практики частный случай МНК, когда модель описывается линейным уравнением (см. выше).
Для простоты описания преобразований пронормируем переменные хij,уi. следующим образом:
где
Тогда
В дальнейшем изложении будем считать, что рассматриваемые переменные пронормированы
описанным образом, и верхние индексы 
опустим. Для облегчения
демонстрации основных идей примем достаточно естественные предположения.
1. Для рассматриваемых переменных существуют следующие пределы:
2. Количество опытов n таково, что можно пользоваться асимптотическими
результатами, полученными при 
3. Погрешности измерения удовлетворяют одному из следующих типов ограничений:
Тип 1. Абсолютные погрешности измерения ограничены согласно (48):
Тип 2. Относительные погрешности измерения ограничены:
Тип 3. Ограничения наложены на сумму погрешностей:
(поскольку все переменные отнормированы, т.е. представляют собой относительные величины, то различие в размерности исходных переменных не влияет на возможность сложения погрешностей).
Перейдем к вычислению нотны оценки МНК. Справедливо равенство:
Воспользуемся следующей теоремой из теории матриц [14].
Теорема. Если функция f(λ) разлагается в степенной ряд в круге сходимости |λ – λ0| < r, т.е.
то это разложение сохраняет силу, если скалярный аргумент заменить любой матрицей А, характеристические числа которой λk, k = 1,…,n, лежат внутри круга сходимости.
 |
Из этой теоремы вытекает, что:
Легко убедиться, что:
Это вытекает из последовательности равенств:
Применим приведенную выше теорему из теории матриц, полагая А = Δ Z и принимая, что собственные числа этой матрицы удовлетворяют неравенству |λk|<1. Тогда получим:
Подставив последнее соотношение в заключение упомянутой теоремы, получим:
Для дальнейшего анализа понадобится вспомогательное утверждение. Исходя из предположений 1-3, докажем, что:
Доказательство. Справедливо равенство
где 
- состоятельные
и несмещенные оценки дисперсий и коэффициентов ковариации, т.е.
тогда
где
Другими словами, каждый элемент матрицы, обозначенной как о(1/n), есть бесконечно малая величина порядка 1/n. Для рассматриваемого случая cov(x) = E, поэтому
Предположим, что n достаточно велико и можно считать, что собственные числа матрицы о(1/n) меньше единицы по модулю, тогда
что и требовалось доказать.
Подставим доказанное асимптотическое соотношение в формулу для приращения b*, получим
Выразим
Δb* относительно приращений ΔХ,
ΔY до 2-ro порядка
Перейдем
от матричной к скалярной форме, опуская индекс (R):
Будем
искать max(|Δbk*|)
по Δxij и Δyi
(i=1,…, п ;j=1,…,
m). Для этого рассмотрим все три ранее введенных типа
ограничений на ошибки измерения.
Тип 1 (абсолютные погрешности измерения ограничены). Тогда:
Тип 2 (относительные погрешности измерения ограничены). Аналогично получим:
Тип
З (ограничения наложены на сумму погрешностей). Предположим, что |Δbk*| достигает максимального значения при таких значениях погрешностей
Δxij и Δyi, которые мы обозначим как:
тогда:
Ввиду линейности последнего выражения и выполнения ограничения типа 3:
Для простоты записей выкладок сделаем следующие замены:
Теперь для достижения поставленной цели можно сформулировать следующую задачу, которая разделяется на m типовых задач оптимизации:
при ограничениях
Перепишем минимизируемые функции в следующем виде:
Очевидно, что fik > 0.
Легко видеть, что
Следовательно, необходимо решить nm задач
при ограничениях "типа равенства":
Сформулирована типовая задача поиска экстремума функции. Она легко решается. Поскольку
то максимальное отклонение МНК-оценки k-ого параметра равно
Кроме рассмотренных выше трех видов ограничений на погрешности могут представлять интерес и другие, но для демонстрации типовых результатов ограничимся только этими тремя видами.
Оценивание линейной корреляционной связи. В качестве примера рассмотрим оценивание линейной корреляционной связи случайных величин у и х1 , х2..., хm с нулевыми математическими ожиданиями. Пусть эта связь описывается соотношением:
где b1 , b2 ,..., bm - постоянные, а случайная величина е некоррелирована с х1 , х2..., хm. Допустим, необходимо оценить неизвестные параметры b1 , b2 ,..., bm по серии независимых испытаний:
Здесь при каждом i = 1,2,…,n имеем новую независимую реализацию рассматриваемых случайных величин. В этой частной схеме оценки наименьших квадратов b1*R , b2*R ,…, bm*R параметров b1, b2 ,..., bm являются, как известно, состоятельными [45].
Пусть величины х1 , х2..., хm в дополнение к попарной независимости имеют единичные дисперсии. Тогда из закона больших чисел [45] следует существование следующих пределов (ср. предположение 1 выше):
где σ - среднее квадратическое отклонение случайной величины е.
Пусть измерения производятся с погрешностями, удовлетворяющими ограничениям типа 1, тогда максимальное приращение величины |Δb*k|, как показано выше, равно:
Перейдем к предельному случаю и выпишем
выражение для нотны:
В качестве примера рассмотрим случай m = 2. Тогда
Приведенное выше выражение для максимального приращения метрологической погрешности не может быть использована в случае m = 1. Для m = 1 выведем выражение для нотны, исходя из соотношения:
Подставив m
= 1, получим:
Следовательно, нотна выглядит так:
Nf=M{|2xb* – y|}Δx+M{|x|}Δy .
Для нахождения рационального объема выборки необходимо сделать следующее.
Этап 1. Выразить зависимость размеров и меры области рассеивания Bα(n,b) от числа опытов n (см. выше).
Этап 2. Ввести меру неопределенности и записать соотношение между статистической и интервальной неопределенностями.
Этап 3. По результатам этапов 1 и 2 получить выражение для рационального объема выборки.
Для выполнения этапа 1 определим область рассеивания следующим образом. Пусть доверительным множеством Bα(n,b) является m-мерный куб со сторонами длиною 2K, для которого
Исследуем случайный вектор b* и
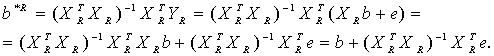
Как известно, если элементы матрицы А = {аij} -случайные, т.е. А – случайная матрица, то ее математическим ожиданием является матрица, составленная из математических ожиданий ее элементов, т.е. М{А} = {М{аij}}.
Утверждение 1. Пусть А = { аij } и В = { bij } - случайные матрицы порядка (m х n) и (n х r) соответственно, причем любая пара их элементов (аij, bkl) состоит из независимых случайных величин. Тогда математическое ожидание произведения матриц равно произведению математических ожиданий сомножителей, т.е. M{AB} = M{A} M{B}.
Доказательство. На основании определения математического ожидания матрицы заключаем, что
,
но так как случайные величины аik, bkj независимы, то
,
что и требовалось доказать.
Утверждение 2. Пусть А = {аij} и В = {bij} - случайные матрицы порядка (m х n) и (n х r) соответственно. Тогда математическое ожидание суммы матриц равно сумме математических ожиданий слагаемых:, т.е. М{А+В} = М{А} + М{В}.
Доказательство. На основании определения математического ожидания матрицы заключаем, что
M{А+В} = {М{аij+bij}} = {М{аij} + М{bij}} =M{A} + M{B},
что и требовалось доказать.
Найдем математическое ожидание и ковариационную матрицу вектора b* с помощью утверждений 1, 2 и выражения для b*R , приведенного выше. Имеем
Но так как M{ e } = 0, то M {b*R} = b . Это означает что оценка МНК является несмещенной.
Найдем ковариационную матрицу:
Как выяснено ранее, для достаточно большого количества опытов n выполняется приближенное равенство
Осталось определить вид распределения вектора b*R . Из выражения для b*R, приведенного выше, и асимптотического соотношения (51) следует, что
Можно утверждать, что вектор b*R имеет асимптотически нормальное распределение, т.е.
Тогда совместная функция плотности распределения вероятностей случайных величин b*R1 , b*R2 ,…, b*Rm будет иметь вид:
где
Тогда справедливы соотношения
Подставим в формулу (52), получим
где
Вычислим асимптотическую вероятность попадания описывающего реальность вектора параметров b в m-мерный куб с длиной стороны, равной 2k, и с центром b*R.
Сделаем замену
Тогда
где Т = (n/2)1/2(k/σ), а Ф0(Т )- интеграл Лапласа,
где 
- функция стандартного
нормального распределения с математическим ожиданием 0 и дисперсией 1. Из последнего
соотношения получаем
Т = Ф-1 (P1/m),
где Ф-1(Р) - обратная функция Лапласа. Отсюда следует, что
k = σ (2/n)1/2 Ф-1 (Р1/m). (53)
Напомним, что доверительная область Bα (n,b) - это m-мерный куб, длина стороны которого равна К, т.е.
P( b ÎBα (n,b))= P (-K <β1<K, -K <β2<K,…, -K <βm<K) = α.
Подставляя P = α в формулу (53), получим
К = k = σ (2/n)1/2 Ф-1(α 1/m ). (54)
Соотношение (54) выражает зависимость размеров доверительной области (т.е. длины ребра куба К) от числа опытов n, среднего квадратического отклонения σ ошибки е и доверительной вероятности α. Это соотношение понадобится для определения рационального объема выборки.
Переходим к этапу 2. Необходимо ввести меру разброса (неопределенности) и установить соотношение между статистической и интервальной (метрологической) неопределенностями с соответствии с ранее сформулированным общим подходом.
Пусть A - некоторое измеримое множество точек в m-мерном евклидовом пространстве, характеризующее неопределенность задания вектора а Î A . Тогда необходимо ввести некую меру М(А), измеряющую степень неопределенности. Такой мерой может служить m-мерный объем V(A) множества А (т.е. его мера Лебега или Жордана), М(А) = V(A).
Пусть P - m-мерный параллелепипед, характеризующий интервальную неопределенность. Длины его сторон равны значениям нотн 2N1, 2N2,…, 2Nm , а центр а (точка пересечений диагоналей параллелепипеда) находится в точке b*R. Пусть C - измеримое множество точек, характеризующее общую неопределенность. В рассматриваемом случае это m-мерный параллелепипед, длины сторон которого равны 2(N1 + K), 2(N2 + K),…, 2(Nm + K), а центр находится в точке b*R . Тогда
M(P)= V(P) = 2m N1 N2… Nm , (55)
M(C) = V(C) = 2m (N1 + K)(N2 + K)…(Nm + K). (56)
Справедливо соотношение (49), согласно которому М(C) = М(P) + М(F), где множество F = C\P характеризует статистическую неопределенность.
На этапе 3 получаем по результатам этапов 1 и 2 выражение для рационального объема выборки. Найдем то число опытов, при котором статистическая неопределенность составит δ 100% от общей неопределенности, т.е. согласно правилу (50)
M(F) = М(C) - М(P) = δ M(C) (57)
где 0 < 
< 1.
Подставив (55) и (56) в (57), получим
Следовательно,
Преобразуем эту формулу:
откуда
Если статистическая погрешность мала относительно метрологической, т.е. величины K/Ni малы, то
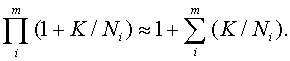
При m = 1 эта формула является точной. Из нее следует, что для дальнейших расчетов можно использовать соотношение
Отсюда нетрудно найти К:
Подставив в формулу (58) зависимость K = K(n), полученную в формуле (54), находим приближенное (асимптотическое) выражение для рационального объема выборки:
При m = 1 эта формула также справедлива, более того, является точной.
Переход от произведения к сумме является обоснованным при
достаточно малом , т.е. при достаточно
малой статистической неопределенности по сравнению с метрологической. В общем
случае можно находить К и затем рациональный
объем выборки тем или иным численным методом.
Пример 1. Представляет интерес определение nрац для случая, когда m = 2, поскольку простейшая линейная регрессия с m =2 широко применяется. В этом случае базовое соотношение имеет вид
(1 + К/N1)(1 + К/N2) = 1/(1 - ).
Решая это уравнение относительно К, получаем
К= 0.5{ -(N1 + N2) + [(N1 + N2)2
+ 4 N1N2 ( /(1 - )]1/2}.
Далее, подставив в формулу (54), получим уравнение для рационального объема выборки в случае m = 2:
σ (2/n)1/2 Ф-1(α1/2)=
0.5{ -(N1 + N2) + [(N1
+ N2)2 + 4 N1N2 ( /(1 - )]1/2}.
Следовательно,
При использовании «принципа уравнивания погрешностей» согласно [3]
При доверительной
вероятности 
имеем 
и согласно [42]
. Для этих численных
значений
Если 
то 
Если же 
то 
Если первое из
этих чисел превышает обычно используемые объемы выборок, то второе находится
в «рабочей зоне» регрессионного анализа.
Парная регрессия. Наиболее простой и одновременно наиболее широко применяемый частный случай парной регрессии рассмотрим подробнее. Модель имеет вид
Здесь xi – значения фактора (независимой переменной),
yi – значения отклика (зависимой
переменной), 
- статистические
погрешности, a, b - неизвестные параметры, оцениваемые
методом наименьших квадратов. Она переходит в модель (используем альтернативную
запись линейной модели)
если положить
Естественно принять, что погрешности факторов описываются матрицей
В рассматриваемой модели интервального метода наименьших квадратов
где X, y – наблюдаемые (т.е. известные статистику)
значения фактора и отклика, XR, yR – истинные
значения переменных, 
- погрешности измерений
переменных. Пусть 
- оценка метода
наименьших квадратов, вычисленная по наблюдаемым значениям переменных,
- аналогичная оценка,
найденная по истинным значениям. В соответствии с ранее проведенными рассуждениями
(59)
с точностью до бесконечно малых более высокого
порядка по 
и 
. В формуле (59)
использовано обозначение 
. Вычислим правую
часть в (59), выделим главный линейный член и найдем нотну.
Легко видеть, что
(60)
где суммирование проводится от 1 до n. Для упрощения обозначений в дальнейшем до конца настоящего пункта не будем указывать эти пределы суммирования. Из (60) вытекает, что
(61)
Легко подсчитать, что
(62)
Положим
Тогда
знаменатель в (61) равен 
. Из (61) и (62)
следует, что
(63)
Здесь и далее опустим индекс i, по которому проводится суммирование. Это не может привести к недоразумению, поскольку всюду суммирование проводится по индексу i в интервале от 1 до n. Из (61) и (63) следует, что
(64)
где
Наконец, вычисляем основной множитель в (59)
(65)
где
Перейдем к
вычислению второго члена с 
в (59). Имеем
(67)
где
Складывая правые
части (65) и (67) и умножая на у, получим окончательный вид члена с
в (59):
(68)
где
(69)
Для вычисления нотны выделим главный линейный член. Сначала найдем частные производные. Имеем
(70)
Если ограничения имеют вид
то максимально
возможное отклонение оценки а* параметра а
из-за погрешностей 
таково:
где производные заданы формулой (70).
Пример
2. Пусть вектор (х,y) имеет двумерное нормальное
распределение с нулевыми математическими ожиданиями, единичными дисперсиями
и коэффициентом корреляции 
. Тогда
(71)
При этом
следовательно,
максимально возможному изменению параметра b* соответствует сдвиг всех xi в одну сторону,
т.е. наличие систематической ошибки при определении х-ов.
В то же время согласно (71) значения в асимптотике выбираются
по правилу
Таким
образом, максимальному изменению а* соответствуют не те , что максимальному
изменению b*. В этом – новое по сравнению с одномерным случаем.
В зависимости от вида ограничений на возможные отклонения, в частности, от вида
метрики в пространстве параметров, будут «согласовываться» отклонения по отдельным
параметрам. Ситуация аналогична той, что возникает в классической математической
статистике в связи с оптимальным оцениванием параметров. Если параметр одномерен,
то ситуация с оцениванием достаточно прозрачна – есть понятие эффективных оценок,
показателем качества оценки является средний квадрат ошибки, а при
ее несмещенности – дисперсия. В случае нескольких
параметров возникает необходимость соизмерить точность оценивания по разным
параметрам. Есть много критериев оптимальности (см., например, [46]), но нет
признанных правил выбора среди них.
Вернемся
к формуле (59). Интересно, что отклонения вектора параметров, вызванные отклонениями
значений факторов и отклика
, входят в (59)
аддитивно. Хотя
но для отдельных компонент (не векторов!) имеет место равенство.
В случае парной регрессии
(72)
Из формул (68), (69) и (72) следует, что
где F и G определены в (69), а
Итак, продемонстрирована возможность применения основных подходов статистики интервальных данных в регрессионном анализе.
| Предыдущая |